「これまではエクセルで計算しなければならなかったことが概算で簡単にイメージできるので取り上げました。コラムに合わせてSNSのフェイスブックやツイッターでも流したのですが、FPの方などにどんどんシェアされるなど反響がありましたね」
その後もネット記事が出たり、FP業界の口コミによる広がりがあったりして、徐々にだが着実に浸透しつつあるのが現状のようだ。
冒頭の問題の答えが「2倍」(3%×42年=126だから、ぴったり法則どおりとなる)と即答できるように、「126の法則」は確かにイメージをつかみやすい。枇々木教授は、
「論文では、この問題の例を出して『積立額は半分で済むと考えるとわかりやすい』としました」
と言う。つまり、冒頭のケースなら老後資金として2千万円を用意したければ積立額は1千万円でよく、3千万円なら積立額は1500万円が必要であることなどがすぐにわかる。枇々木教授は、
「ベースとなる考え方を示せたので、あとはいろいろな活用法をFPの人たちを中心に考えてほしい」
とする。
まず考えられるのが、「72の法則」と同様の使い方だろう。一定の利率を決めれば積立額が2倍になる年数がわかるし、逆に積立期間を想定すれば2倍にするのに必要な利率がわかる。
老後資金に詳しいフィンウェル研究所の野尻哲史所長は、「126の法則」にひと手間加えてさまざまなケースで実際の「月額投資(積立)額」がいくらになるかを導き出した。
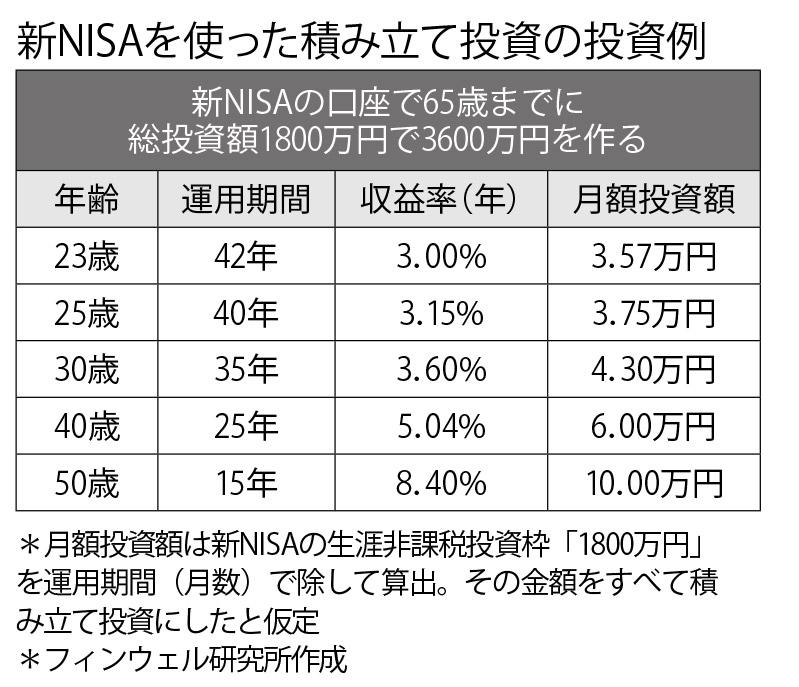
「ちょうど昨年暮れに新NISAの制度拡充が発表され、生涯非課税投資枠が1800万円となったので、それを使ってみました」
例えば、冒頭の問題のケース(利率3%、積立期間42年)なら、総投資額(積立額)1800万円で3600万円を作ろうと思ったら、毎月の積立額は「3.57万円」になる。同様に、25歳から始めて積立期間が40年なら利率は3.15%が必要になり、積立額は「3.75万円」だ。




































