では、「同じであるけれど同じではない」をつじつまを合わせて論理的に説明することはできるでしょうか？「万物の根源は原子である」という原子論を唱えた古代ギリシャのデモクリトスは、同じような矛盾に立ち向かった哲学者でした。次の図を見てください。　

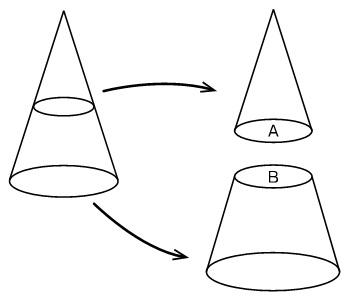
　上の図のように円すいを半分に切ったとき、断面Aと断面Bの面積は同じでしょうか？それとも違うでしょうか？ この問いもいままでたくさんの人と考えてきましたが、「同じ」という意見と「違う」という意見はだいたい半々くらいです。

　同じ派の意見は「断面なんだから面積は同じ」というもので、違う派は「まったく同じなら円柱になるはずで、ほんのわずかでも上が小さいはず」というものや、「刃物には厚さがあり、切った際に必ずすこし削れるはずだから上のほうが小さい」という意見が多いのですが、どうですか？

　どちらの意見も納得がいくものですよね。議論してもらうと、やっぱり平行線になってしまいます。この問題には、簡単な解決方法があります。それは、論理的に考えたり意見を伝えたりするために最も重要なことなのですが、「前提を共有する」ということです。

　つまり、「数学的には同じだけれど、物理的には違う」、あるいは「理論的には同じだけれど、現実的には違う」と言えばよいんです。　

　人は論理的に感じるかどうかで正しさを判断しがちなのですが、そのときに前提を伝え忘れることが多いんです。だから中学生のぼくも原子同士は「物質的には同じだけれど、空間的には違う」というふうに言えばよかったんですね。　
　もう一つ例を挙げます。ぼくが小学生のときにどうしても納得がいかなかったことに、こんな問題があります。「3分の1」を小数に直すと、「0.3333……」と永遠に続きます。では両方に3をかけるとどうなるでしょうか？「1」と「0.9999……」になります。この二つを同じといってよいでしょうか？

次のページ
「同じ」ということにしないと成り立たない